गति, चाल, दूरी, और वेग की कुछ महत्वपूर्ण बातें जो आपको परीक्षा में भी काम आयेगी

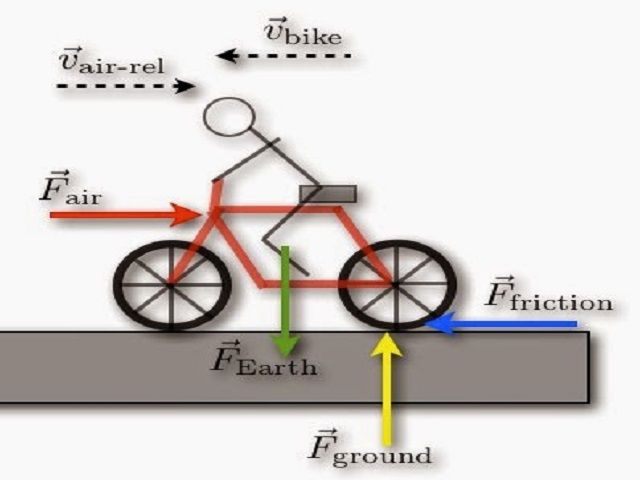
गति (motion)

अदिश राशि (scalar quantity ): वैसी भौतिक राशि, जिनमें केवल परिमाण होता है. दिशा नहीं, उसे अदिश राशि कहा जाता है: जैसे - द्रव्यमान, चाल , आयतन, कार्य , समय, ऊर्जा आदि.
नोट: विद्युत धारा (current), ताप (temprature), दाब (pressure) ये सभी अदिश राशियां हैं.

सदिश राशि (vector quantity): वैसी भौतिक राशि जिनमें परिमाण के साथ-साथ दिशा भी रहती है और जो योग के निश्चित नियमों के अनुसार जोड़ी जाती हैं, उन्हें संदिश राशि कहते हैं: जैसे- वेग, विस्थपान, बल, त्वरण आदि.

दूरी (distance): किसी दिए गए समयान्तराल में वस्तु द्वारा तय किए गए मार्ग की लंबाई को दूरी कहते हैं. यह एक अदिश राशि है. यह सदैव धनात्मक (+ve) होती हैं.

विस्थापन (displacement): एक निश्चित दिशा में दो बिन्दुओं के बीच की लंबवत दूरी को विस्थापित कहते है. यह सदिश राशि है. इसका S.I. मात्रक मीटर है. विस्थापन धनात्मक, ऋणात्मक और शून्य कुछ भी हो सकता है.

चाल (speed): किसी वस्तु के विस्थापन की दर को चाल कहते हैं. अथार्त चाल = दूरी / समय यह एक अदिश राशि है. इसका S.I. मात्रक मी./से. है.

वेग (velocity ): किसी वस्तु के विस्थापन की दर को या एक निश्चित दिशा में प्रति सेकंड वस्तु द्वारा तय की दूरी को वेग कहते हैं. यह एक सदिश राशि है. इसका S.I. मात्रक मी./से. है.

त्वरण (acceleration): किसी वस्तु के वेग में परिवर्तन की दर को त्वरण कहते हैं. इसका S.I. मात्रक मी/से^ 2 है. यदि समय के साथ वस्तु का वेग घटता है तो त्वरण ऋणात्मक होता है, जिसे मंदन (retardation ) कहते हैं.

वृत्तीय गति (circular motion ) - जब कोई वस्तु किसी वृताकार मार्ग पर गति करती है, तो उसकी गति को वृत्तीय गति कहते हैं. यदि वह एक समान चाल से गति करती है तो उसकी गति को एक समान वृत्तीय गति कहते हैं.

समरूप वृत्तीय गति एक त्वरित गति होती है क्योंकि वेग की दिशा प्रत्येक बिंदु बदल जाती है.

कोणीय वेग (circular and motion) वृताकार मार्ग पर गतिशील कण को वृत के केंद्र से मिलाने वाली रेखा एक सेकंड में जितने कोण से घूम जाती है, उसे उस कण का कोणीय वेग कहते हैं. इसे अकसर ω (ओमेगा) से प्रकट किया जाता हैं. यानी कि ω = Ѳ / t . यदि कण 1 सेकंड में n चक्कर लगाता हैं तो, ω = 2π n.
(क्योंकि 1 चक्कर में कण 2π (360 डिग्री) रेडियन से घूम जाती है) अब यदि वृताकार मार्ग की त्रिज्या r  है और कण 1 सेकंड में n चक्कर लगाता है तो उसके द्वारा एक सेकंड में चली गई दूरी = वृत्त की परिधि x n = 2 πrn, यही उसकी रेखीय चाल (linear speed) होगी. 
यानी कि v = 2 πrn
v = 2π n x r = ω x r ( ω =2 π n )
रेखीय चाल = कोणीय चाल x त्रिज्या.